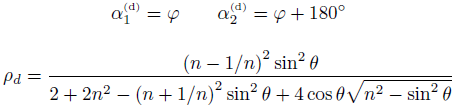|
Home Publications York Polarisation Photometric stereo Q-Bot Composites Theory 1 Theory 2 Theory 3 Theory 4 Polarization and Reflection in ImagesPerhaps the most common exploitation of polarization in computer vision is to measure the polarization state of light reflected from dielectric surfaces [1]. Natural light undergoes partial polarization when it is reflected from surfaces. Consider a specular reflection being viewed through a rotating polarizer. Because the electric field of the reflected wave is most attenuated in the plane of reflection, greatest transmission through the polarizer occurs when it is oriented at right angles to the plane. Minimum transmission occurs when the polarizer is parallel to the plane. Note however, that the polarizer is unable to distinguish two planes of reflection oriented 180° apart. If α is the azimuth angle of the surface (the angle of the projection of the surface normal onto the image plane), then there are two possible values for a given measurement of φ:
where the superscript s indicates that the reflection is specular. The Fresnel Equations can be used to represent the maximum and minimum intensities passing through a rotating polarizer:
Here R|| and R⊥ are the parallel and perpendicular Fresnel intensity reflectivity components respectively, n is the refractive index, θ is the angle of incidence and Ir is the magnitude of the specularity. In an imaging situation, θ is equivalent to the zenith angle of the surface (the angle between the surface normal and the line of sight of the camera). Re-writing in terms of the degree of polarization and rearranging gives:
where the suffix s is appended to the degree of polarization as this assumes a purely specular reflection. This theory allow one to impose constraints on the angle of a reflecting surface for shape recovery applications using measurements taken of φ and ρ. Apart from at the Brewster angle, where ρ=1, there are also two solutions to this equation, meaning two zenith angles are also possible. The azimuth angle of the surface also has two possibilities as shown by the equation at the top of the page (and the graph on the previous page). Combining the above theory with the subsurface scattering model of reflection [1, 2], the following relations for diffuse reflection can derived:
On this occasion, there is only one solution for the zenith angle, but the degree of polarization is lower and therefore more difficult to measure. Indeed, the information contained in this degree of polarization is only useful where the zenith angle is large [3]. References[1] Wolff, L.B., Boult, T.E. (1991). Constraining object features using a polarisation reflectance model. IEEE Trans. Patt. Anal. Mach. Intell. 13, 635-657. [2] Wolff, L.B. (1994). Diffuse reflectance model for smooth dielectric surfaces. J. Opt. Soc. Am. A 11, 2956-2968. [3] Atkinson, G. A. , Hancock, E. R. (2006). Recovery of Surface Orientation from Diffuse Polarization. IEEE Trans. Im. Proc. 15,1653-1664. |