CP502: Representations for Graphs.

5.5. Representations for Graphs.

What information does a graph possess?


      vertices         and their names

      edges            and their labels/ weights

      direction        of the arc

      connectivity     how many edges at each node.

This can give us information such as:


        Is it possible to go from Perth to Hobart by train?

        Is the circuit diagram totally connected or is a component

                dangling unconnected?

        What is the shortest/ fastest/ cheapest route from A to B?

The appropriate choice of data structure depends upon the operation to be performed on the vertices/ arcs and whether the graph is dense or sparse.

Also depends upon whether we want all the information above to be stored explicitly. If the vertex names are mapped into integers 1..V then a square matrix [1..V,1..V] can be constructed which shows the adjacency of each node: i.e A[x,y] is TRUE or has a value(=weight) if there is an edge between node x and node y. Note a direct line not a path. It is FALSE or has an "unconnected" value otherwise.


         P    M    S    N    H    L    C

  P      1    1    0    0    0    0    0

  M      1    1    1    0    0    0    1  COST

  S      0    1    1    1    0    0    1         A    B    C

  N      0    0    1    1    0    0    0     A   0   inf  10

  H      0    0    0    0    1    1    0     B  inf   0    5

  L      0    0    0    0    1    1    0     C  10    5    0

  C      0    1    1    0    0    0    1

Note it is symmetric but if graph is directed then it may not be. Note if arcs have weights/ costs/ values these can be substituted.


Cost of 0 to not go (ie journey to place you are at) and

infinite cost to go to someplace you cannot go

( no rail service from Canberra to Hobart).

This then would require:


        array[1..V,1..V] of boolean;          or

        array[1..V,1..V] of weights/values/costs;

If we want to store the names as well then we need an array of records. Notice that we now have V-squared storage locations even if graph has few arcs (sparse). This means that our algorithms to read in and process may be O(V-squared).

An example of the use of the matrix is :

Can we go from PERTH to HOBART?


      Test a[P,H]. 0=>no direct link.

      What of indirect links?

            Test a[P,M]. 1 => we can go to Melbourne.

                Test a[M,H]. 0=> not from Melbourne.

            Test a[P,S]. 0  => not to Sydney.

            Test a[P,N]. 0  => not to Newcastle.

            Test a[P,L]. 0  => not to Launceston.

            Test a[P,C]. 0  => not to Canberra.

Finally, after our exhaustive search, we find that no path exists from Perth to Hobart.

To avoid this O(V-squared) problem we can use an adjacency list rather than a matrix to hold the graph.

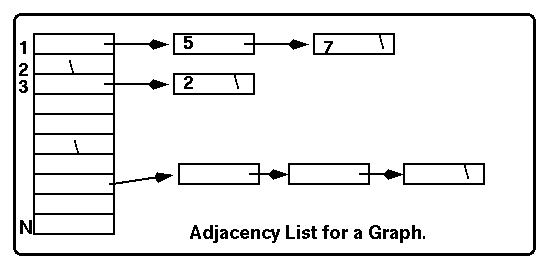
Note that this indicates that an edge occurs between nodes 1 and 5 and nodes 1 and 7. An edge occurs between 3 and 2 but not between 2 and 3: it represents a directed graph. Now our algorithm to create the list need not be O(V-squared) and depends on whether it is a directed graph and how sparse or dense it is. As before other information can be added to represent weights, etc. Surprise!!

5.5.1. Depth First Search.

Many of our original questions about graphs can be answered by traversing the graph. A Depth-First algorithm can be used for this. In doing this we must keep track of every vertex visited: we use an array [1..V] of (visited,not_visited). Initially we set the entire array to not_visited and then systematically visit each node and set to visited.

Alternatively we may wish to initialise the array to 0 and then visit the n-th node and set array[node] = n.


      begin

             n  0;

            for k   1 to v do  matrix[k]  0;

            for k   1 to v do

                   if matrix[k] = 0 then visit(k)

      end;

Procedure visit recursively examines all nodes connected to the node that was passed to it: hence the name depth first search.


 procedure visit(integer k);

 var

       t:integer;

 begin

       n  n+1;

       matrix[k]  n;

       for t  1 to v do

              if a[k,t] then

                 /* use adjacency matrix to determine

                          which node to visit next.    */

                   if matrix[t] = 0 then

                           /* Not visited yet therefore: */

                                     visit(t);

 end;

Note that this is O(V-squared) whereas the linked list would be O(V+E) since we set V matrix values and examine each edge E.

Question: does a graph have a cycle?


We get the answer from visit:

iff a non-zero matrix entry is discovered in visit procedure.

That is, we find an edge that has already been visited.

Question: is the graph connected?


Each non-recursive call to visit corresponds to a different

connected component. All connected nodes are visited at each

recursive call because the visit algorithm searches out

all connected nodes!!!

To see if Hobart can be reached from Perth, start search at Perth (or Hobart) and see if Hobart (or Perth) is recursively seen. That is, connected.

5.5.2. Breadth-First Search.

There is also a breadth-first search algorithm. Rather than go as deep(recursively) as you can down the graph structure and then work back upwards, we would visit each node at the top "level" , and then each node at next level, etc The two algorithms are good for different applications and analysis of each can be found in most standard text books.