5.3. Graphs.   

A graph is a common Abstract Data Type used to represent many models: it is a finite set of points connected or unconnected by lines.
Example: A good example of a graph is cities and the transport routes between the cities.  

transport_graph.eps 

Notice that Hobart and Launceston are part of one graph but

are not connected to other links. This would be true in reality

if we were concerned with Rail transport.

Example: A state table: indicates our present environment and possible new environments or states we can progress to.  

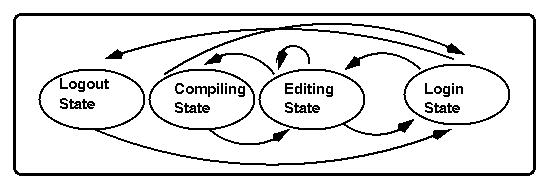
state_table_graph.eps 

Note we can only go in one direction on certain links:

once we have logged off, we can only login again.

Also we cannot login twice on the one terminal.

This is called a directed graph or digraph.

(An operating system is a huge state machine.)

Nomenclature for graphs is rich (and unfortunately varied).
Nodes, Vertices, Points: these are just the points on the graph. They can have labels or names as well as other parameters. The node would probably be represented as a record of information in Java. They represent a state of the total configuration: a login state or being in Perth (State of Excitement).
Edges, Arcs, Lines: connections between two vertices. It can be directed (one way) or undirected (two way). A directed arc or edge is (more formally) an ordered pair of vertices (a,b): a is called the tail and b is called the head. Arc(a,b) ===> a --> b

This is for a directed graph.
Path: a sequence of vertices v1, v2, ... vn such that

v1 --> v2, v2 --> v3
are arcs. Path is from v1 to vn. 


Note that the geometrical representation of a graph may bear

little relationship to its mathematical nature.

I could put Hobart next to Perth and Sydney south of Melbourne.

 A graph just tells us vertices(and their labels)

and arcs (and their weights).

If an arc is labelled, the graph is a labelled graph. If all nodes/arcs in a path are distinct except for the first and last then the path is simple. A path that ends up where it starts is cyclic.

Connected/Unconnected: A graph is connected if there is a path from every node to every other node. An unconnected graph has no paths from every node to every other node.

Trees: A graph with no cycles is a tree. A tree has a node plus zero or more children. Therefore there is only one path between any two nodes in a tree.  

tree_graph.eps

If we add an edge to a complete tree, it must form a cycle.