CP502: Recursion Principle.

5.2. Recursion Principle.

Always start a recursive algorithm by testing for trivial cases and handle these non-recursively.

Note:

(1) A recursive procedure/function must have some way of stopping its recursion else it will call itself forever.

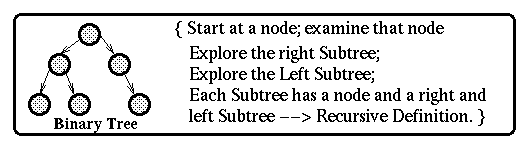
(2) Some algorithms are ideally suited to a recursive solution, especially problems concerned with complex data structures such as trees.

Some algorithms only look as though they are ideally suited to recursive techniques. They turn out to be much less efficient than iterative solutions. Times for factorial.




       Recursive factorial: 478 m sec. Iterative : 230 msec.

Rule of thumb is that if a non-recursive version can be written which is only slightly larger than recursive version, then use the non-recursive version.

(3)


       If RECURSIVE, then

        (i)   Isolate terminating condition and value.

        (ii)  Work out how recursive parameters are to be manipulated

              on each call.

Consider ways of avoiding too many recursive calls. Minimise number of parameters since these and local variables must be STACKed on each call.

Recursion is a useful tool when dealing with many data structures.